Print every possible sub-sequence in an array.

You are a programmer and you have been given an integer array, and your task is to print every possible sub-sequence but each sub-sequence should be in order i.e. left -> right.

What the hell do I mean by every possible sub-sequence?

Let’s say the array contains 3 elements in it, example {5,2,1}. And if you google the word subsequence you will get something like this

a sequence that can be derived from the given sequence by deleting some or no elements without changing the order of the remaining elements.

yes I also copied and pasted it, anyways continuing to the topic so for an array {5,2,1} the possible sub-sequence will be

{5,2,1}
{5,2}
{5,1}
{5}
{2,1}
{2}
{1}
{}

where each sequence is in order that is from left to right. {1,5} can’t be a sub-sequence because it's not in the order.

And in order to confirm that those 8 sub-sequences which we wrote above are all the possible sequences, there is a formula to check the number of sub-sequence that can be formed on any sequence and that is 2^n where n is the number of elements in an array or in items in that sequence.

Now we don’t have to understand how this formula works, we are programmers, not mathematicians.

And for the sequence of 3, we get 8 by applying this formula which is by the way nothing but (2*2*2).

Now how to write a program which can print all the possible sub-sequence for n elements?

I don’t know about you, but when I hear the word “every sub-sequence” there is only one algorithm that comes to my mind and that is Recursion.

Now let me give you a heart attack by showing you the code directly.

Output of below code

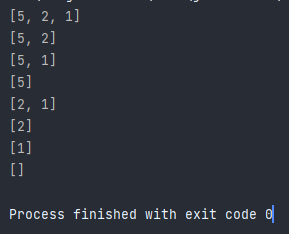
Let's understand the code first but not the flow of it yet.

we have created an array and pre-initialized it with {5,2,1}, after that i have created an empty linked list which will be used to store every possible sequence and after that, we are calling a function printEverySubSequence and passing it the following arguments

0 — — — — -> which is the first index of the array

arr — — — --> array itself

size — — — -> size of that array which will be 3 in this case

tempList — -> empty linked list which we created.

Now the printEverySubSequence function, where the actual magic is happing.

The key point in the printEverySubSequence function is, that we are starting from the first element and forming every possible sequence which can be formed by that first index and then moving to the next index and repeating the cycle again.

And in order to get all the possible subsequences on that first element, we have to make two choices either to pick that element or to leave/ignore it.

For example, if I have an array {5,2,1}, and if I take the first element 5 I have two choices either I can take the 5 or I can leave it. And since we have to form every sub-sequence why not make both the choices separately. And after making both the choice we move forward in the array by incrementing our index value by 1 and applying the same thing to the two newly generated choices/sequences which got created by making those two choices and repeating the cycle again.

Here is a recursion tree to understand it visually.

In this recursion tree, each level is representing an index of the array, level 1 is index 0, level 2 is index 1 and the last level represents index 2. And the leaf nodes or the yellow highlighted sets are the possible sequences that we can have for the array {5,2,1}.

And in the printEverySubSequence, we are making these two choices by first adding the current index element into the tempList (which is our first choice) and then calling the printEverySubSequence function again with that tempList and incremented index. And once it returns back from that sub-recursion we remove the element from the tempList which is our second choice and call the printEverySubSequence function again with the tempList and again index with an incremation of 1.

And for the base case on each recursion call, we are checking if the index is greater or equal to the size, and if it is we print the current tempList and return.

Time complexity will be O(2^n)

Space complexity will be O(n)

If you learned anything from this article please press that follow button

if (!already)🚗